Spatial Search

Choochoo includes a pure-Python RTree implementation (Guttman 1984).

This can be used as a stand-alone library:

from ch2.rtree import CLRTree, CQRTree, CERTree

(for Cartesian points, linear, quadratic and exponential split, respectively).

If it would be useful I can separate this code into it’s own package - please contact me.

• Design
• Minimum Bounding Rectangles
• Points as Data
• Other API Details
• Split Algorithm
• Latitude / Longitude
• Efficiency
• Extension

Design

The API evolved considerably to meet the following requirements:

• Provide Python-like, intuitive defaults.
• Support location data as values as well as keys.
• Avoid 3rd-party dependencies or complex algorithms for polygon intersection.

The result provides:

• Default methods (including __getitem__, __setitem__, keys, values and items) that provide a map from points to multiple values:

  > tree = CQRTree()
  > square = ((0,0),(0,1),(1,1),(1,0))
  > tree[square] = 'square'
  > tree[square]
  <iterator...>
  > list(tree[square])
  ['square']
  > square in tree
  True
  > diagonal = ((0,0),(1,1))
  > list(tree[diagonal])
  []
  > diagonal in tree
  False
  > list(tree.keys())
  [((0,0),(0,1),(1,1),(1,0))]
  > list(tree.values())
  ['square']
  > list(tree.items())
  > [(((0,0),(0,1),(1,1),(1,0)), 'square')]
  > len(tree)
  1
  > del tree[square]
  > len(tree)
  0
  

• Extended retrieval based on MBRs (minimum bounding rectangles):

  > tree = CQRTree(default_match=MatchType.INTERSECTS)
  > tree[square] = 'square'
  > list(tree[diagonal])
  ['square']
  

• The possibility to retrieve points (keys) as well as values:

  > tree = CQRTree(default_match=MatchType.INTERSECTS)
  > tree[square] = 'square'
  > list(tree.get_items(diagonal))
  [(((0,0),(0,1),(1,1),(1,0)), 'square')]
  

Minimum Bounding Rectangles

Internally, the tree works with MBRs in Cartesian coordinates:

(x_low_left, y_low_left, x_high_right, y_high_right)

Storage takes a list of (x, y) points, constructs the MBR, and saves the original points together with the value in a leaf node.

So, for example, add() can be called with a single point [(x, y)], a rectangle [(x1, y1), (x2, y2)] or a polygon [(x1, y1), (x2, y2), ...].

Queries (and deletions) support four match types:

• EQUALS - the request exactly matches the points in the tree (including point order).
• CONTAINED - the MBR of the request is contained within the MBR of the points in the tree.
• CONTAINS - the MBR of the request contains the MBR of the points in the tree.
• INTERSECTS - the MBR of the request intersects with the MBR of the points in the tree.

In all cases, multiple results may be returned (as an iterator). Similarly, a single deletion may remove multiple (or no) entries.

Note that the default EQUALS retrieval returns values only where the points match. Other retrieval modes ignore the points and work only with the MBR.

Points as Data

Since the points may be important as values (as well as keys) they are returned by get_items().

The value parameter can be used to label different spatial datasets:

for points in dataset_1: tree.add(points, 1)
for points in dataset 2: tree.add(points, 2)
# query for dataset_1 points in the given region
tree.get_item(region, value=1, match=MatchType.CONTAINS)
# delete all dataset_2 points
tree.delete(tree.global_mbr, value=2, match=MatchType.CONTAINS)

(but note that the deletion may be less efficient than filtering .items() and rebuilding the tree).

Other API Details

The constructor (and add_all()) can take an iterable of (points, value) pairs (as generated by .items()).

Any value can be stored. Neither keys not values need be unique.

Use delete_one() to remove only the first match found. Match order may change when data are added or removed.

Modifying the tree while iterating over contents is unsafe (and should trigger an error).

The border parameter, which can also be set as a global default on the constructor, extends MBRs (on addition and query if set globally). This might be useful for approximate matching.

In the final API, MBRs are never visible to the caller.

IMPORTANT - if you are using this for approximate retrieval don’t forget to st default_match in the constructor. The default is for exact matching.

Split Algorithm

All three algorithms from the paper are implemented. As can be seen from the figures below, quadratic gives results close to exponential and consistently better than linear.

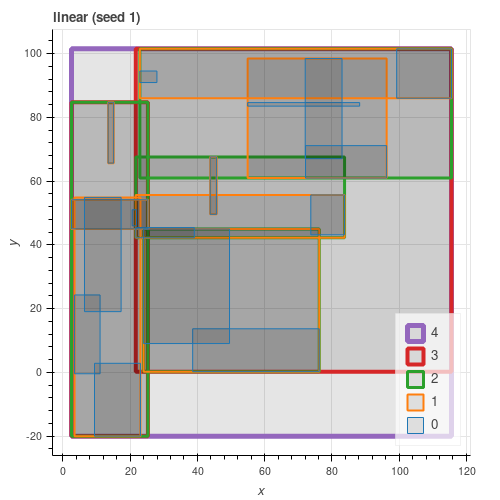
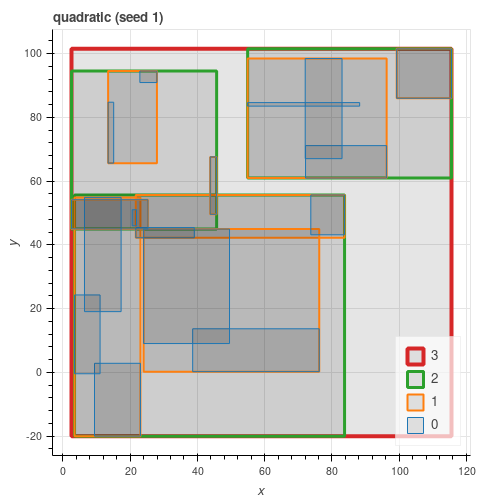
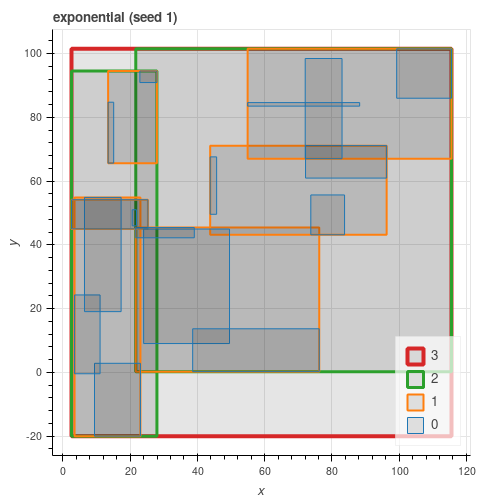
Latitude / Longitude

Basic RTree assumes Cartesian coordinates.

To provide minimal support for local latitude / longitude the LLRTree, LQRTree and LERTree classes subtract the initial longitude and normalize to (-180, 180] on input, reversing the transform on output.

Longitude is “x”, latitude “y”.

With this normalization, longitude should work correctly provided data do not cover more than half the available range.

No correction is made to latitude - this will not work correctly when overlapping the poles.

This could also work with phase, or any other angular measure in degrees.

Efficiency

Profiling suggests that most time is spent comparing MBRs (evaluating max() and min()). This occurs on descent and argues for small (more discriminatory) nodes. This is supported by timing tests across different entry sizes - max_entries of 3 appears optimal.

Exponential split is slower than quadratic or linear at any entry size.

Extension

The tree was designed for further extension via mixins. Please see the code.